Wie erhält man aus zwei Punkten die Zuordnungsvorschrift der linearen Funktion?
Von der Zuordnungsvorschrift f(x) = m x + c ist die Steigung m und der y-Achsenabschnitt c zu bestimmen.

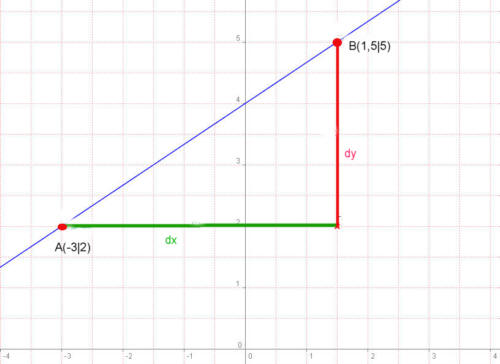
Berechne zunächst die Steigung m = dy / dx = [ By - Ay ] / [ Bx - Ax ]
In dem im Bild dargestellten Beispiel ist m = [ By - Ay ] / [ Bx - Ax ] = [ 5 - 2 ] / [ 1,5 - (-3) ]= 3 / 4,5= 2 / 3
Von der Zuordnungvorschrift ist nun bereits die Steigung m bekannt und lässt sich einsetzen. f(x)= (2/3) x + c
Um auch den y-Achsenabschnitt c zu bestimmen, setzt man die Koordinaten von einem der gegebenen Punkte
in die Zuordnungsvorschrift ein und erhält eine Gleichung, die nur noch nach c aufzulösen ist.
Aus dem Beispiel wurden die Koordinaten von A in die Zuordnungsvorschrift eingesetzt.
f(-3)=2=(2/3)*(-3)+c
2=-2+c
4=c
Die vollständige Zuordnungsvorschrift aus dem Beispiel lautet also:
f(x)=(2/3) x +4